Durante 25 domingos a partir del 13 de octubre de 2019 se publicarán en el periódico El Día un problema matemático cuya solución será publicada dos semanas después en este web. Antes puedes enviar tu respuesta a 50math@ull.edu.es. Entre los participantes se sorteará una calculadora CASIO (entidad que colabora con esta iniciativa) y un lote de libros editados por la Federación Española de Sociedades de Profesores de Matemáticas (FESPM) por cada problema. También en esta web publicaremos a los ganadores. Los premios se entregaran el 26 de junio en el acto de clausura de la celebración de los 50 años de estudios de Matemáticas en la ULL.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 1 (del 13/10/2019): Hay 3 cofres, uno con monedas de oro en su interior, otro con monedas de plata y un tercero con ambas cosas. Cada cofre tiene un cartel: uno pone ORO, otro PLATA y el otro ORO Y PLATA y sabemos que los tres carteles están mal colocados.
Solo puedes tomar una moneda de una cesta para identificar qué caja es cada una, ¿qué harías?
Solución: Tomar una moneda de la cesta que pone “ORO Y PLATA”. Si es de oro, ya sabes que ese cofre solo tiene monedas de oro. Si es de plata, pues es el cofre de monedas de plata. Ahora es fácil identificar los otros dos cofres.
Ganadores:Ibai Noda Martín (premio una calculadora Casio) y Gregorio Rodríguez Pérez (premio libros)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 2 (del 20/10/2019): Utiliza los 10 dígitos (0,1,2,…,8,9) para formar dos números de 5 cifras tal que su diferencia sea lo más pequeña posible.
SOLUCIÓN: 50123 – 49876 = 247. Para que la diferencia sea mínima, la diferencia entre el primer dígito de cada número (las decenas de millar) debe ser 1. Después hay que buscar que el número mayor sea lo más pequeño posible y el número menor sea lo más grande posible. Así que el número mayor debería terminar en 0123 y el número menor en 9876 (solución de Moisés García)
Ganadores: Dácil Pérez (premio una calculadora Casio) y Carlos Ledesma Hernández (premio libros)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 3 (del 27/10/2019): Tienes 25 caballos y quieres averiguar cuáles son los 3 más rápidos. Para ello puedes organizar carreras en las que corren 5 caballos de tu elección.¿Cuántas carreras necesitas para saber cuáles son los tres caballos más rápidos?
SOLUCIÓN: Con 7 carreras se puede solucionar. Divides los 25 caballos en grupos de 5 y organizas esas 5 carreras. Después organizas una sexta carrera y tomando al ganador de cada una de estas cinco, si llamamos A, B, C, D y E a los caballos de esta carrera por orden de llegada. El caballo A es el más rápido de todos. Si te fijas bien, solo hay 5 caballos candidatos a ser segundo y tercero más rápidos (los caballos B y C, los que quedaron segundo y tercero en la primera carrera con A y el que quedó segundo en la primera carrera con B). Así que organizando una última carrera con estos cinco se resuelve el problema.
Ganadores: Thalía García Villamil (premio una calculadora Casio) y Juset Gil (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 4 (del 03/11/2019): Hay 5 cajas numeradas del 1 al 5. Cada noche el gato duerme en una caja adyacente a la de la noche anterior. Cada mañana puedes abrir una caja y mirar si el gato está dentro. ¿Cuantos días necesitas para estar seguro de encontrar al gato?
SOLUCIÓN: 6 días. Si abres las cajas en el siguiente orden: 2, 3, 4, 2, 3, 4 verás cómo no hay forma de que el gato escape. Además, en 5 días no se puede conseguir.
Ganadores: Alonso Yanes Estévez (premio una calculadora Casio) y Lara González Barrios (premio libros)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
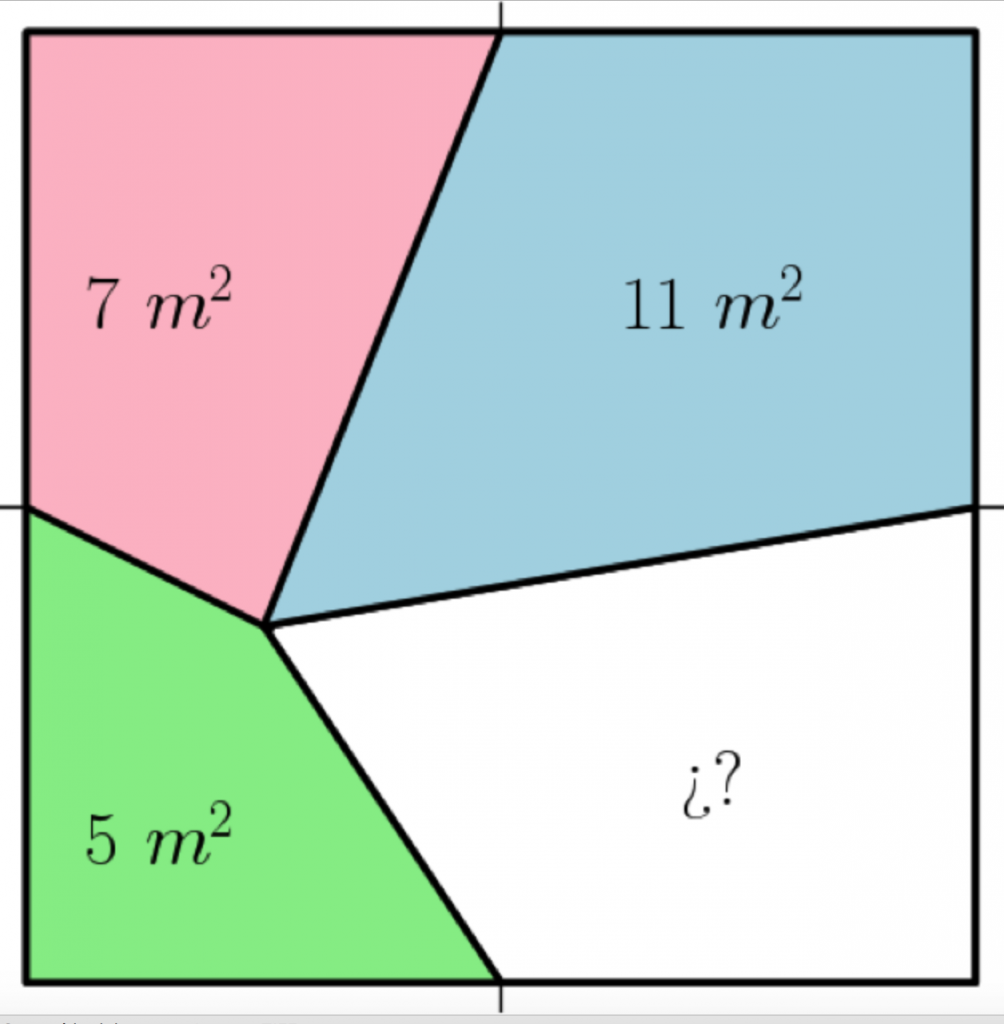
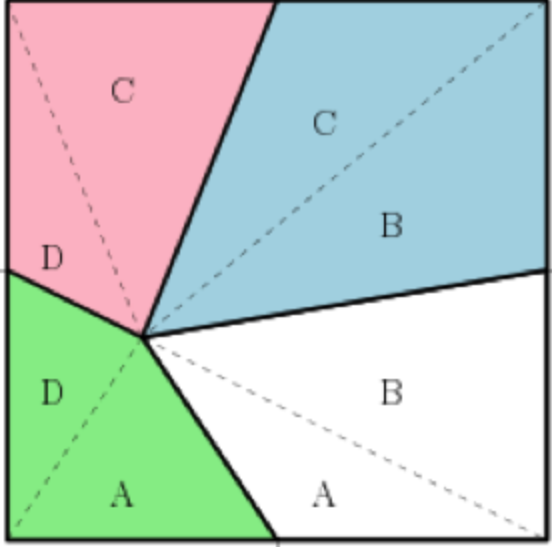
Problema 5 (del 10/11/2019): Tenemos un cuadrado en el que hemos marcado los puntos medios de cada lado y lo hemos dividido en cuatro regiones como muestra la figura ¿Cuál es el área marcada en blanco?
SOLUCIÓN:
Si dividimos cada región en dos triángulos, se observa que los triángulos marcados con la misma letra tienen misma base y misma altura y, por tanto, misma área.
X = A + B = A + D + B + C + D –C –D = Área Verde + Área Azul – Área Rosa = 9m2
Ganadores: Eva Perera González (premio una calculadora Casio) y Salvador Jover (premio libros)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 6 (del 17/11/2019):
Entré en una cafetería y me dispuse a leer el periódico El Día. Observé que tenía 60 páginas y deduje que estaba compuesto de 15 hojas grandes que se doblan por la mitad.
Cuando me marchaba del bar, me llevé la página que tenía el Sudoku para hacerlo en casa. Si el Sudoku estaba en la página 53 ¿qué otras tres páginas me llevé?
SOLUCIÓN: me llevé las páginas 7, 8 y 54.
Ganadores: Elena Griñén (premio una calculadora Casio) y Raúl Jesús Linares Abad (premio libros)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 7 (del 25/11/2019):
Tenemos un saco con 24 kilos de arena y una balanza de platillos como la de la figura ¿cómo podemos hacer para coger exactamente 9 kilos de arena?
SOLUCIÓN: si repartimos la arena en los dos platillos de forma que queden equilibrados, habremos separado dos montones de 12 kg en cada. Si repetimos el proceso con uno de los montones de 12kg, podemos conseguir 6 kg en cada platillo y, si lo hacemos una tercera vez, separaremos 3kg. Si un montón de 6 kg con uno de 3kg, tendremos los 9kg que queríamos.
Ganadores:Itahisa Melián González (premio una calculadora Casio) y Fernando Muñoz (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 8 (del 02/12/2019):
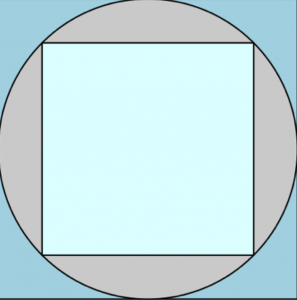
Sin medir los lados ¿cuál es la relación entre el área del cuadrado grande y del cuadrado pequeño?
SOLUCIÓN: El área del cuadrado grande es el doble que la del pequeño. Basta con girar el cuadrado pequeño 45 grados para observarlo.
Ganadores: Ana Moreno (premio una calculadora Casio) y Ibai Noda Martín (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 9 (del 09/12/2019):
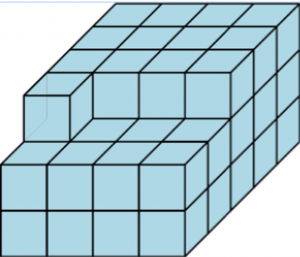
Juntando cubitos pequeños de 1x1x1 formamos la figura del dibujo.
Luego, pintamos el exterior de la figura con pintura azul y después separamos todos los cubos pequeños ¿cuántos tendrán las cuatro caras pintadas? ¿y tres? ¿y dos? ¿y una? ¿y ninguna?
SOLUCIÓN: Hay un cubo con 4 caras pintadas, 9 cubos con 3 caras pintadas, 22 cubos con 2 caras pintadas, 17 cubos con una cara pintada y 4 sin ninguna cara pintada.
Ganadores: Francisco Morales Villegas(premio una calculadora Casio) y Ana Perera González (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 10 (del 16/12/2019):
Tengo un triángulo con lados A, B y C. Cuando mido el lado A más el lado B, me da 12cm. Cuando mido el lado A más el lado C, me da 11 cm. Finalmente, mido el lado B más el lado C y me da 9 cm.”
¿Cuál es el perímetro del triángulo?
SOLUCIÓN: Si sumamos 12 cm + 11 cm + 9 cm = 32 cm estamos sumando dos veces cada lado y, por tanto el perímetro del triángulo es de 32/2 = 16 cm.
Ganadores:Omar Oudeh Mishmesh (premio una calculadora Casio) y Dahiana Cappetta Braojos (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 11 (del 23/12/2019):
El director de una comparsa es muy amante del orden. Un día, en un ensayo, decide formar a los bailarines en filas de 4, pero se da cuenta de que le sobra uno. Lo intenta con filas de 6 y también le sobra un bailarín. Una vez más, lo intenta con filas de 5 y le sigue sobrando uno. Si la comparsa tiene menos de 100 bailarines ¿Cuántos fueron al ensayo?
SOLUCIÓN: Si hubiese venido una persona menos, el número de personas sería múltiplo 4, de 5 y de 6 y, por tanto múltiplo de 60. Como hay menos de 100 bailarines, la única opción es que fueran 61.
Ganadores: Boris Bagemihl (premio una calculadora Casio) y Sofía López Herrera (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 12 (del 30/12/2019):
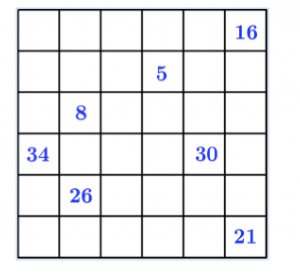
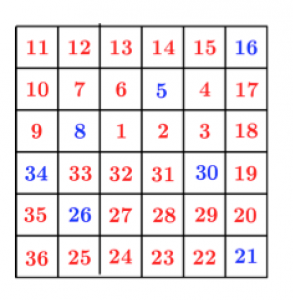
Un perro podenco recorrió todas las casillas de un campo cuadriculado. Avanzaba en horizontal y vertical. Empezó en la casilla con el número 1 y fue numerándolas desde allí sucesivamente. Reconstruye el recorrido
Ganadores: Bárbara Mesa (premio una calculadora Casio) y Saúl Cabrera García (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 13 (del 06/01/2020):
Mi primo es muy supersticioso y no le gusta el número 13. Es por eso que cuando tuvo que escoger una contraseña de 4 dígitos para el banco, no quiso poner el 3 inmediatamente después del 1 ¿cuántas contraseñas distintas pudo haber elegido mi primo?
SOLUCIÓN: Hay 9701 contraseñas posibles. Contemos cuántas no son posibles:
– todas aquellas que sean de la forma 13xy, que hay 100;
– las de la forma x13y, que también hay 100, y
– las de la forma xy13, que hay 100.
No obstante, la contraseña 1313 la hemos contado dos veces (en el primer caso y en el tercero), es por eso que hay 299 contraseñas prohibidas dentro de un total de 10000 y 10000 – 299 = 9701.
Ganadores: Salvador Jover (premio una calculadora Casio) y Gregorio Rodríguez Pérez (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 14 (del 13/01/2020):
Un número es “capicúa” si se lee igual de izquierda a derecha que de derecha a izquierda. Por ejemplo, el 17071 es un número capicúa de 5 dígitos. Este nombre proviene del catalán, donde “cap i cua” significa “cabeza y cola”. Pero:
¿Hay más números capicúas de tres dígitos o bien de cuatro dígitos?
SOLUCIÓN: Hay el mismo número. Para convencerte de esto piensa, por ejemplo ¿cuántos números capicúas de 3 dígitos hay que terminen en 25? En efecto, solo hay uno, el 525. De igual forma solo hay un número capicúa de 4 dígitos que acabe en 25, el 5225.
Ganadores: Laura Valls Antos (premio una calculadora Casio) José Luis Rodríguez González (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 15 (del 20/01/2020):
Sobre dos caras del cubo de Rubik de mi hermana dibujé con rotulador blanco las diagonales que se ven en la imagen. ¿De cuántos grados es el ángulo que forman esos segmentos?
SOLUCIÓN: 60 grados. Pintando la línea azul del dibujo se forma un triángulo equilátero.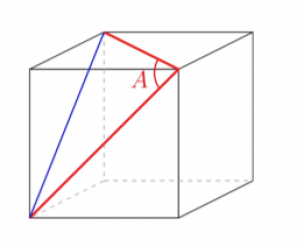
Ganadores: Jose Luis Rodriguez González (premio una calculadora Casio) Gerardo Rodríguez (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 16 (del 27/01/2020):
Este finde me fui al cumpleaños de una amiga. Había doce pasteles y en total éramos doce personas. Si hubo quien comió dos pasteles, quien comió medio pastel y quien solo comió un cuarto de pastel. ¿De qué forma se repartieron los pasteles?
SOLUCIÓN: 4 personas comieron dos pasteles, una persona comió medio pastel y 6 personas comieron un cuarto de pastel.
Ganadores: Lucía Díaz González (premio una calculadora Casio), Francesco La Spina (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 17 (del 03/02/2020):
Un número es “autobiográfico” si, empezando por la izquierda, su primera cifra indica el número de ceros del número, su segunda cifra el número de unos, etc. Por ejemplo, el número 2020 es autobiográfico porque tiene 2 ceros, 0 unos, 2 doses y 0 treses.
Hay un único número autobiográfico de diez dígitos ¿cuál es?
SOLUCIÓN: El 6210001000
Ganadores: Manolo Aguilar Topham (premio una calculadora Casio), Laura Francisco Rodríguez (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 18 (del 10/02/2020):
Si tienes los números del 10 al 1 en orden descendente, es decir:
10 , 9 , 8 , 7 , 6 , … , 2 , 1
Sin cambiar el orden de los números, ¿cómo podrías obtener el número 2020 añadiendo entre ellos únicamente paréntesis y los símbolos aritméticos de la suma, resta y multiplicación?
Ejemplo: el número 2000 se puede conseguir de la siguiente forma:
2000 = 10 x (9 + 8 – 7) x (6 + 5 + 4 + 3 + 2) x 1
SOLUCIÓN: 2020 = 10 x 9 x 8 + (7 + 6) x 5 x 4 x (3 + 2) x 1
Ganadores: Yazmin Geve (premio una calculadora Casio), Sergio Méndez Dévora (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 19 (del 17/02/2020):
El mítico CD Tenerife de la temporada 96/97 tenía 7 delanteros. En los partidos en que el míster, Jupp Heynckes, decidía alinear tres delanteros, siempre lo hacía con las siguientes restricciones. Si ponía a Juanele o a Felipe, tenía que alinear también al otro porque se entendían muy bien en el campo. Sin embargo, cuando alineaba a Kodro no debía poner a Pinilla, porque jugaban en la misma zona. ¿Cuántas posibles delanteras podía formar?
SOLUCIÓN: Con Juanele y Felipe hay 5 posibles. Sin estos dos jugadores quedan 5, con los que pueden formar 10 tripletas. De estas 10 hay que quitar en las que coincidan Kodro y Pinilla, que son exactamente 3. En total hay 5 + 10 – 3 = 12 posibles delanteras.
Ganadores: Astrid Cardona (premio una calculadora Casio) y Javier Benito (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 20 (del 24/02/2020):
Un año es bisiesto si cumple una de estas condiciones:
- Es múltiplo de 400
- Es múltiplo de 4, pero no de 100.
Teniendo esto en cuenta ¿Cuántos años bisiestos ha habido desde el año 1 de nuestra era hasta el actual 2020?
SOLUCIÓN: En los todos los meses de este año (que es bisiesto), el dígito 2 aparece en los números 2, 12, 20, 21, 22 (2 veces), 23, …, 29; es decir, 13 veces. Esto hace un total de 13 x 12 = 156 veces.
Ganadores: Amaia Alcalde Gimili (premio una calculadora Casio) y Jose Fernández (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 21 (del 02/03/2020):
¿Cuánto mide la mesa?
SOLUCIÓN: 150 cm
Ganadores: Dayana Pérez (premio una calculadora Casio) y Rubens Hernández (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 22 (del 09/03/2020):
Tienes ocho pilas de las cuales cuatro están cargadas y cuatro descargadas. Si tu robot necesita dos pilas cargadas y tienes siete intentos para ponerlo a funcionar. ¿Cómo lo harías?
SOLUCIÓN: Una combinación posible es: 12, 23, 13, 45, 56, 46, 78.
Si al menos dos de las pilas numeradas con 1, 2 y 3 están cargadas, entonces en uno de los primeros tres intentos el juguete funcionará.
De igual forma, si al menos dos de las pilas numeradas con 4, 5 y 6 están cargadas, entonces en uno de los intentos del cuarto al sexto el juguete funcionará. En caso contrario, las pilas 7 y 8 están cargadas y el juguete funcionará en el último intento.
Ganadores: Lara González Barrios (premio una calculadora Casio) y Alonso Yanes Estévez (premio libros).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 23 (del 16/03/2020):
Un saltamontes puede saltar hacia la izquierda o hacia la derecha. En el primer salto avanza un centímetro, en el segundo dos centímetros y así sucesivamente, aumentando un centímetro en cada salto… Tras treinta saltos, ¿puede terminar donde empezó?
SOLUCIÓN: No, tras 30 saltos siempre acabará a un número impar de centímetros de donde empezó.
Ganadores:Javier Benito (premio una calculadora Casio) y Miguel Ángel Aballe Villero (premio libros)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 24 (del 23/03/2020):
Enrique pintó siete puntos en un folio de forma que no había tres en la misma línea recta. Maite observó que usando tres puntos cualesquiera de los que había dibujado Enrique, se puede pintar un triángulo que los tiene como vértices. Y Santiago se entretuvo dibujando los treinta y cinco triángulos. Elena se preguntó: ¿Puede haber una línea recta que toque todos los triángulos?
SOLUCIÓN: No, una recta divide el folio en dos partes y puede pasar como mucho por dos de los puntos dibujados. De los (al menos) 5 puntos restantes, habrá al menos 3 en uno de los dos lados y, por tanto, el triángulo que los tiene como vértices no es tocado por la recta.
Ganadores: Alonso Yanes Estévez (premio una calculadora Casio) y Lara De La Cruz González Barrios (premio libros)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Problema 25 (del 30/03/2020):
La décima espinela, ya sea recitada, escrita o cantada (punto cubano), está muy presente en la tradición canaria. Para terminar esta serie de problemas los dejo con uno planteado en esta estrofa poética. ¡Que lo disfruten!
Ochenta duros tenía
pa unas quícaras comprar
y en La Zarza pude dar
con un viejo que vendía.
Para aprovechar el día
tantas quícaras compré
como pesetas pagué
por cada una, con gusto,
si el dinero me dio justo
¿cuántas quícaras llevé?
SOLUCIÓN: 20 quícaras
Ganadores:Christian Maggio (premio una calculadora Casio) y Julián Pacheco Fernández (premio libros)




Deja una respuesta